# Imaginary Number
# Colorized Definition
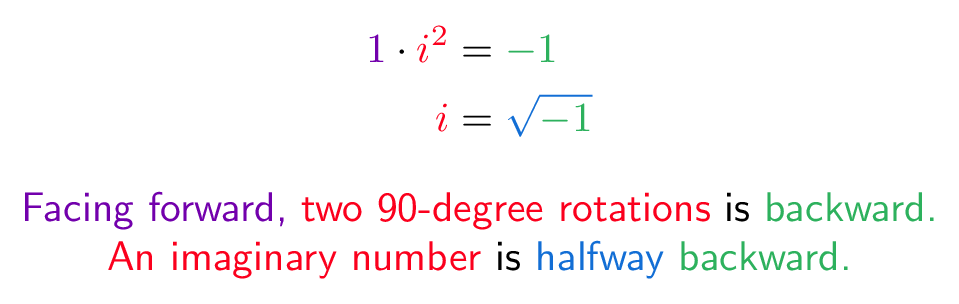
\newcommand{\forward}{\color{c1}}
\newcommand{\backward}{\color{c2}}
\newcommand{\sideways}{\color{c3}}
\newcommand{\halfway}{\color{c4}}
\newcommand{\combo}{\color{c5}}
\begin{equation*}
\begin{split}
\forward 1 \plain \cdot \sideways i^2 &= \backward -1 \\
\sideways i &= \halfway \sqrt{ \backward -1 }
\end{split}
\end{equation*}
\forward Facing forward, \sideways two 90-degree rotations \plain is \backward backward. \\
\sideways An imaginary number \plain is \halfway halfway \backward backward.
# Plain English
What's an imaginary number? A number pointing sideways (North/South) isntead of the typical East/West number line. ("Imaginary" was a derogatory name from critics, Gauss wanted them called "lateral" numbers.)
What does i mean? i, by itself, points North. Multiplying by i rotates you 90 degrees. 2 rotations points you backwards (i * i = -1), 4 rotations spins you around fully (i^4 = 1).
Is i useful? The second dimension is useful, right? Imaginary numbers make 2d rotation problems simple.