# Euler's Identity
# Colorized Definition
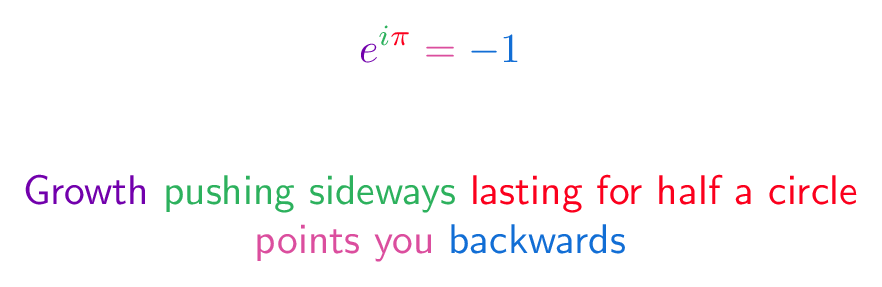
\newcommand{\growth}{\color{c1}}
\newcommand{\rotation}{\color{c2}}
\renewcommand{\time}{\color{c3}}
\newcommand{\real}{\color{c4}}
\newcommand{\imaginary}{\color{c5}}
\newcommand{\location}{\color{c6}}
$$\growth e^{\rotation i \time \pi} \plain \location = \real -1$$
\growth Growth
\rotation pushing sideways
\time lasting for half a circle
\\
\location points you
\real backwards